중등 – 피타고라스 정리
피타고라스 정리

오늘은 피타고라스 정리의 증명 여섯번째 방법에 대해서 설명 하겠습니다.

이 방법은 피타고라스가 증명한 넓이를 이용한 증명법입니다. 가장 기초적이면서도 직관적이고, 쉬운 증명 방법 입니다.
피타고라스 정리 증명(피타고라스 방법)
step 1
아래 사각형을 잘 관찰해 보세요.
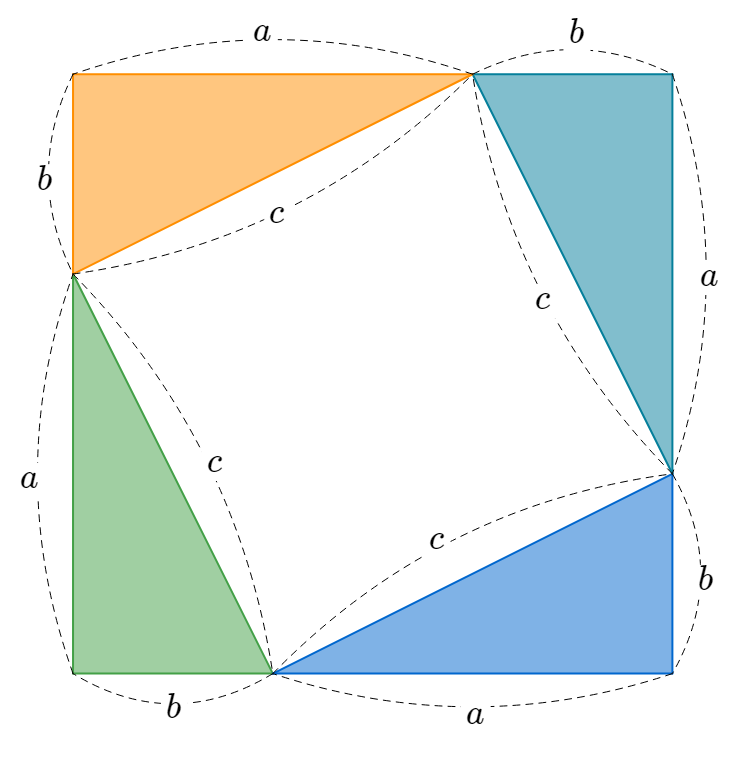
위 그림은 \( a + b \) 를 한 변으로 하는 정사각형을 만들기 위해 직각삼각형 네개를 꼭짓점이 맞닿도록 배치 한 그림 입니다.
step 2
이렇게 하면 전체 큰 정사각형의 넓이와 직각삼각형 4개 + 가운데 정사각형의 넓이의 합이 서로 같게 됩니다. 즉,
\[ (a+b)^2 = 4 \times \frac{1}{2}ab + c^ 2 \] 이 성립 하게 됩니다.
이것을 정리하면
\[ a^2 + 2ab + b^2 = 2ab + c^2 \]
\[ a^2 + b^2 = c^2 \]
step 3
이로써 \(a^2 + b^2 = c^2 \) 임을 증명하였습니다.
마무리
오늘은 피타고라스 정리 6번째 증명에 대해서 설명 드렸습니다.
이 증명 방법은 피타고라스 본인의 증명 방법이기 때문에 의미가 있는것 같습니다. 이 방법은 가장 기초적이면서도 쉬운 방법 중 하나 입니다.
다음에 더 재미있는 방법의 증명방법에 대해서 소개 드리도록 하겠습니다.
