피타고라스 정리

오늘은 피타고라스 정리의 증명 다섯번째 방법에 대해서 설명 하겠습니다.

이 방법은 미국 제20대 대통령인 제임스 A. 가필드가 찾은 방법 입니다. 보통은 직각삼각형 각 변의 길이를 한변으로 하는 정사각형으로 피타고라스 정리를 증명하는데 가필드는 같은 직각삼각형을 조합해서 다른 도형을 만들어 증명 하였습니다. 이제 가필드가 찾은 피타고라스 증명 방법에 대해서 함께 감상해 보세요.
피타고라스 정리 증명(가필드 방법)
step 1
아래 사각형을 잘 관찰해 보세요.
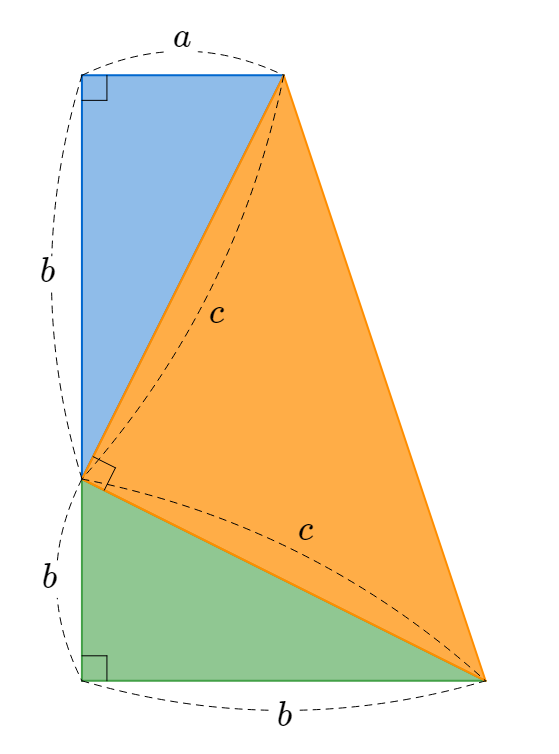
피타고라스 정리를 증명하는 것은 \( a^2 + b^2 = c^2 \) 임을 증명 하는 것입니다.
위 그림에서 피타고라스 정리를 찾아 보도록 하겠습니다.
step 2
기본적인 아이디어는 아래와 같습니다.
위 그림에서 전체 도형의 모양은 사다리꼴 입니다. 이 사다리꼴은 3개의 직각 삼각형의 조합으로 되어 있습니다. 이때 작은 직각삼각형 2개는 서로 합동인 삼각형이고 큰 삼각형 1개는 직각이등변 삼각형 입니다.
step 3
전체 사다리꼴의 넓이는
\[ S_1 = (a+b)\times (a+b) \times \frac{1}{2} \]
입니다.
또한 각 삼각형 3개의 넓이의 합은 아래와 같습니다.
\[ S_2 =\frac{1}{2} ab + \frac{1}{2} ab + \frac{1}{2} c^2 \]
입니다.
\(S_1 = S_2 \) 이므로 아래 식이 성립함을 알 수 있습니다.
\[ (a+b)\times (a+b) \times \frac{1}{2} = \frac{1}{2} ab + \frac{1}{2} ab + \frac{1}{2} c^2 \]
위 식을 정리하면 최종적으로 \(a^2 + b^2 = c^2 \) 식을 유도 할 수 있습니다.
이로써 \(a^2 + b^2 = c^2 \) 임을 증명하였습니다.
마무리
오늘은 피타고라스 정리 5번째 증명에 대해서 설명 드렸습니다.
가필드 증명법은 전문수학자가 아닌 미국 대통령이 증명했다는 점에서 재미있으면서도 특이한 증명법인것 같습니다.
다음에 더 재미있는 방법의 증명방법에 대해서 소개 드리도록 하겠습니다.
