피타고라스 정리

오늘은 피타고라스 정리의 증명 네번째 방법에 대해서 설명 하겠습니다. 피타고라스 정리를 증명하는 방법 중 가장 직관적인 방법은 작은 두개의 정사각형을 자르고 붙여서 큰 정사각형의 넓이과 같다는것을 보이는 방법 입니다. 이 방법은 중등 과정을 진행하고 있는 학생에게도 큰 무리 없이 이해 시킬 수 있습니다. 도형을 유한번 자르고 붙였을 때 원래의 넓이가 보존된다는 성질을 이용하는 것입니다. 이러한 증명법으로는 뵈트헤르(J. E. Böttcher)의 증명과 유희(劉徽)의 증명이 있지만, 오늘은 듀드니 증명법을 소개해 드리도록 하겠습니다.
피타고라스 정리 증명
step 1
아래 사각형을 잘 관찰해 보세요.
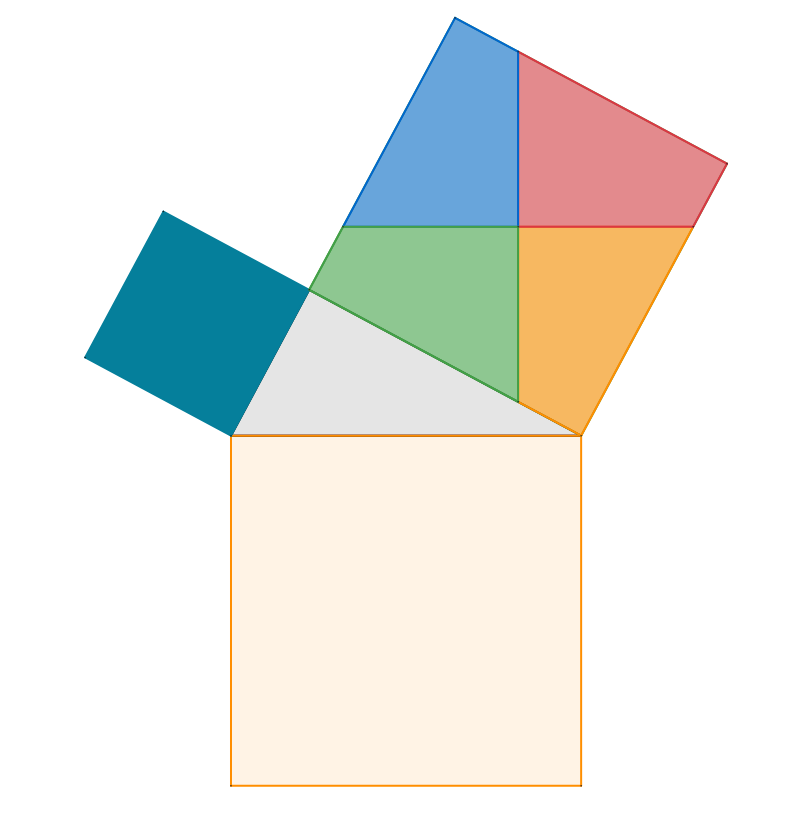
피타고라스 정리를 증명하는 것은 \( a^2 + b^2 = c^2 \) 임을 증명 하는 것입니다.
위 그림에서 위에 있는 작은 사각형 넓이 2개가 아래 있는 큰 사각형 1개의 넓이와 같음을 증명하면 됩니다. 이제 위의 사각형 두개를 잘 잘라서 아래 큰 사각형에 딱 맞게 붙여 넣어 보겠습니다.
step 2
위에 있는 사각형을 자르는 방법은 아래의 방법을 따르면 됩니다.
먼저 사각형의 대각선의 교점으로 무게중심을 찾은 다음 무개중심을 지나는 수직수평 방향의 선분을 그려서 4조각으로 분할 합니다.
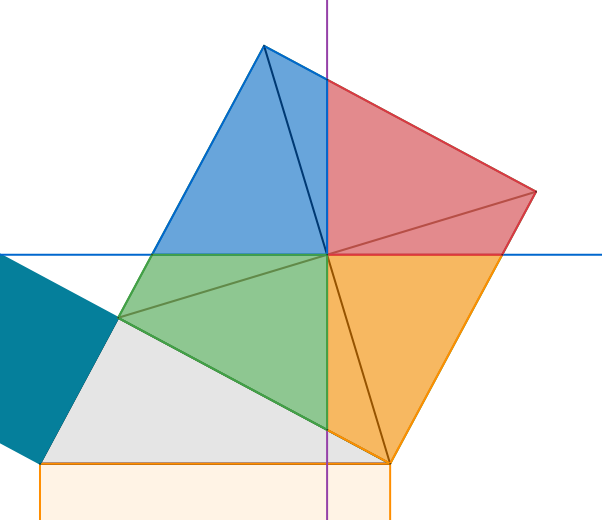
분할된 사각형 4개를 아래 큰 사각형에 잘 맞게 넣어 줍니다.
그리고 작은 사각형 1개를 중앙에 위치 시키면 됩니다.

step 3
위의 2개의 사각형이 아래의 큰 사각형 1개의 넓이와 일치함을 알 수 있습니다.
아래 동영상을 참고해보세요.
이것은 직각삼각형의 변의 길이에 관계 없이 항상 성립함을 알 수 있습니다.
이로써 \(a^2 + b^2 = c^2 \) 임을 증명하였습니다.
마무리
오늘은 피타고라스 정리 4번째 증명에 대해서 설명 드렸습니다.
다음에 더 재미있는 방법의 증명방법에 대해서 소개 드리도록 하겠습니다.
