중등 – 피타고라스 정리
피타고라스 정리

오늘은 피타고라스 정리의 증명 두번째 방법에 대해서 설명 하겠습니다. 이 증명 방법도 역시 중학교 2학년 수준에서 이해하기 쉬운 방법으로 증명하도록 하겠습니다.
피타고라스 정리는 직각 삼각형의 변들 사이의 관계를 설명합니다. 그러나 이것이 왜 성립하는지, 그리고 어떻게 증명할 수 있는지를 이해하는 것은 더욱 중요합니다. 이것이 바로 도형으로 증명하는 이유입니다.
이 포스트에서, 우리는 도형을 통해 피타고라스 정리를 증명할 것입니다. 우리는 직각 삼각형을 그림으로 나타내고, 그것의 각 변들의 길이와 면적을 살펴볼 것입니다. 이를 통해 피타고라스 정리가 왜 성립하는지를 이해할 것입니다.
여러분과 함께 직각 삼각형의 각 변과 면적을 살펴보고, 도형적 증명을 통해 피타고라스 정리의 아름다움을 발견해 보겠습니다.
피타고라스 정리 증명
step 1
아래 사각형을 잘 관찰해 보세요.
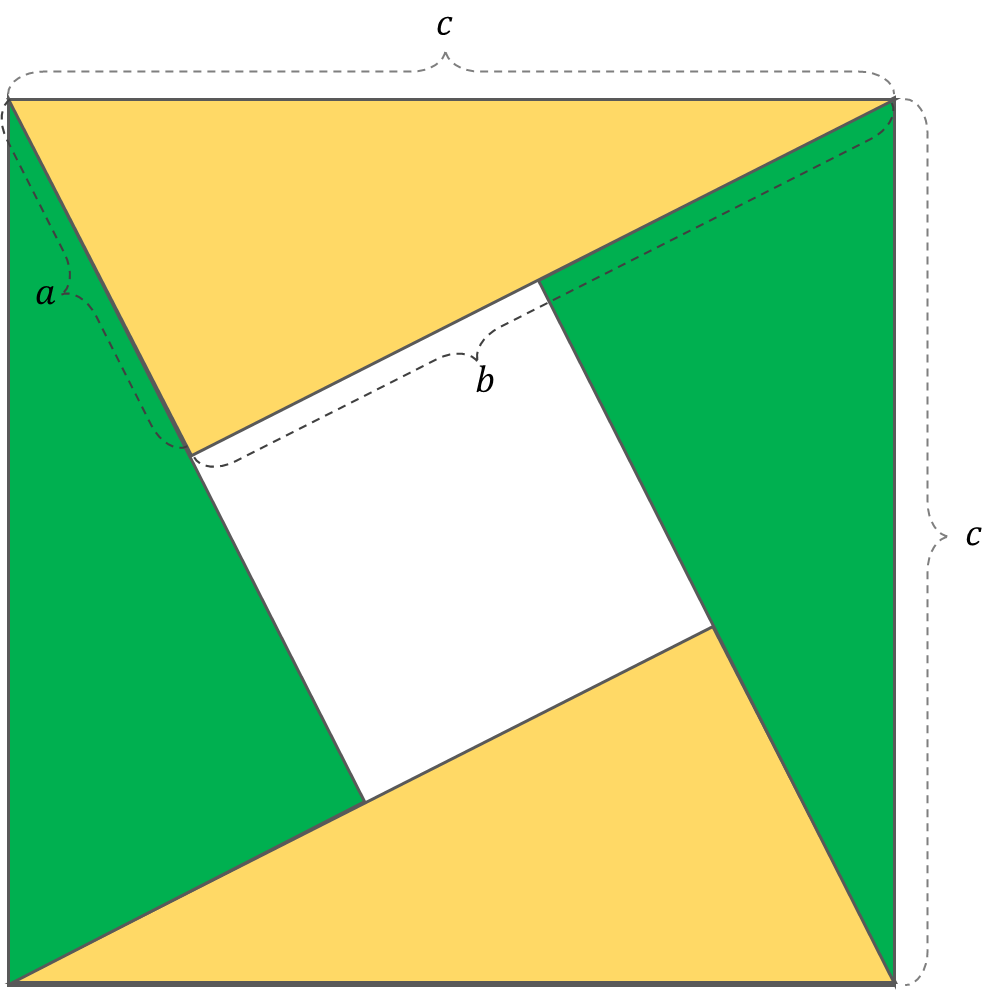
색칠되어 있는 영역의 넓이는 \( c^2 – (a-b)^2 \) 입니다.
step 2
이번에는 아래 사각형을 잘 관찰해 보세요.
이 그림에서 색칠되어 있는 영역의 넓이는 \( 2ab \) 입니다.
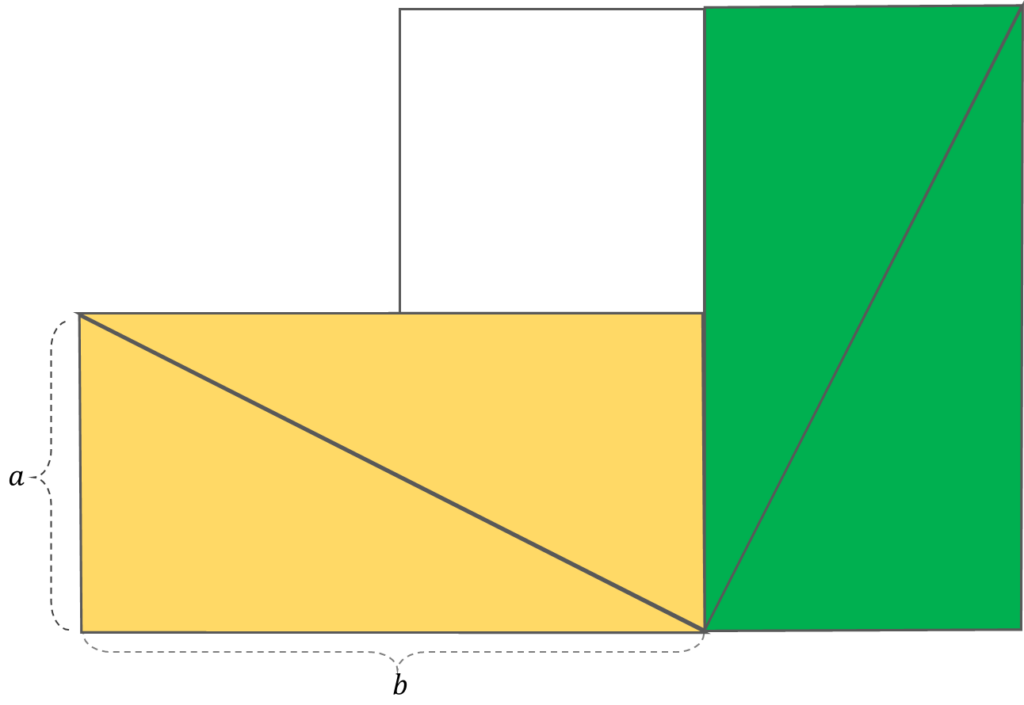
step 3
두 영역의 넓이가 같으니 아래와 같은 식을 얻을 수 있습니다.
\[ c^2 – (a-b)^2 = 2ab \]
이 식을 정리하면 \( c^2 = a^2 + b^2 \) 입니다.
이로서 피타고라스 정리가 증명 되었습니다.
아래 영상을 보면서 위 증명 방법에 대해서 고민해 보시기 바랍니다.
