고등과정 절대부등식 중 코시-슈바르츠 부등식에 대한 기하학적 증명입니다.
코시-슈바르츠 부등식이란?

코시-슈바르츠 부등식 증명(도형)
아래 그림을 자세히 살펴보면서 증명방법을 고민해 보세요.
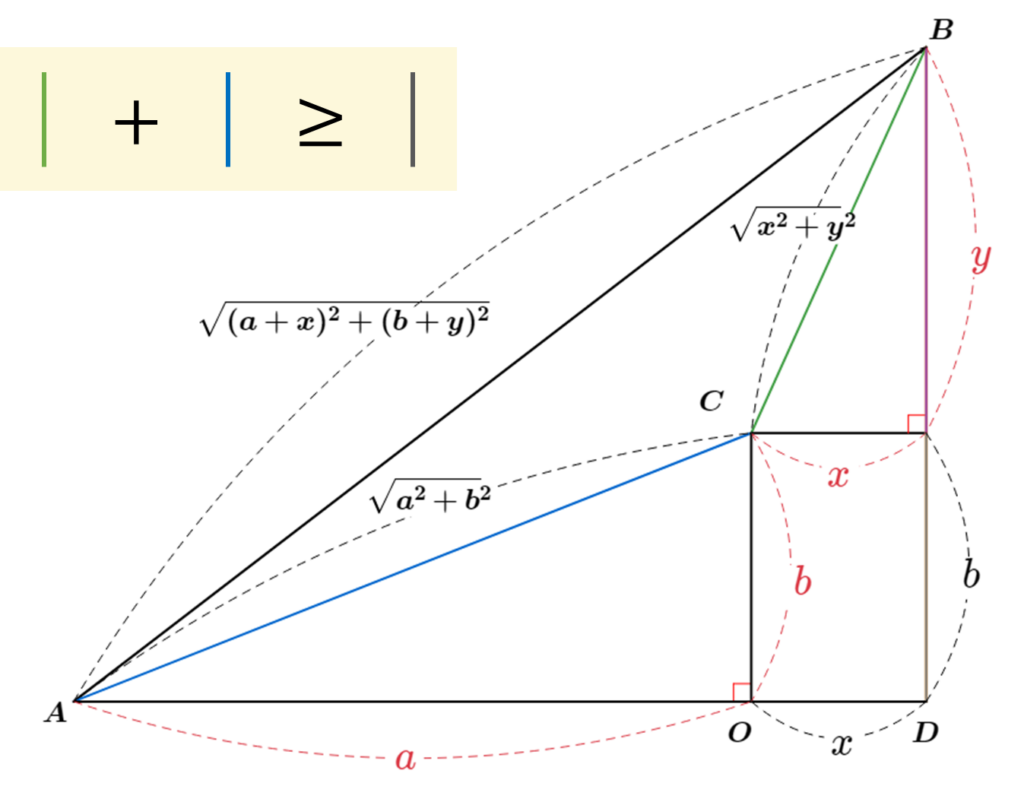
\( \sqrt{x^2 + y^2} + \sqrt{a^2 + b^2} \geq \sqrt{(a+x)^2 + (b+y)^2}\) 가 성립함을 직관적으로 알 수 있습니다.
이제 이 식의 양변을 제곱해서 정리하면 코시-슈바르츠 부등식이 증명 되었습니다.
두번째 증명 방법
아래 이미지의 좌측 도형과 우측 도형은 가운데 사각형의 넓이를 제외하면 둘의 넓이는 동일 합니다. 가운데 사각형의 각 변의 길이는 모두 같습니다. 각 삼각형의 빗변을 사각형의 한 변으로 설정 했기 때문 입니다.
그렇다면 각 변의 길이가 같을 경우 넓이는 어떻게 될까요? 두 변의 길이가 같을 때 변의 사이각이 90도일 경우 삼각형의 넓이는 최대가 됩니다.
즉, 우측 도형의 전체 넓이는 좌측 도형의 전체 넓이보다 크거나 같다는걸 알 수 있습니다.
우측 직사각형의 넓이는
\[ \sqrt{a^2 + b^2 } \sqrt{x^2 + y^2 } \]
입니다.
또한 좌측 평행사변형의 넓이는
\[ (|a| + |y| ) (|b| + |x| ) – 2 \left( \frac{1}{2} |ab| + \frac{1}{2} |xy| \right) = |ax| + |by| \\ |ax + by | \leq |ax| + |by| 이므로 \\ (|a| + |y|)(|b| + |x|) – 2 \left( \frac{1}{2} |ab| + \frac{1}{2} |xy| \right) = |ax| + |by | \geq |ax+by| \] 임을 알 수 있습니다.
우측 직사각형의 넓이는
\[ \sqrt{a^2 + b^2} \sqrt{x^2 + y^2} \]
입니다.
결론적으로 우측의 사각형의 넓이는 좌측 사각형의 넓이보다 크거나 같으니 아래와 같은 식이 성립함을 알 수 있습니다.
\[ \sqrt{a^2 + b^2} \sqrt{x^2 + y^2} \geq |ax + by| \]
양변을 제곱하면
\[ (a^2 +b^2 ) (x^2 + y^2 ) \geq (ax+by)^2 \]
이것으로 코시-슈바르츠 부등식의 기하학적 증명이 완료되었습니다.
