삼각함수 덧셈정리

오늘은 삼각함수 덧셈정리를 증명해 보도록 하겠습니다.
삼각함수의 덧셈정리는 \( \sin, \cos, \tan \) 각각 덧셈정리가 있지만 오늘은 \( \sin \) 의 덧셈정리에 대해서 증명하도록 하겠습니다.
사인의 덧셈정리 증명은 아래 그림에서 시작 합니다.
먼저 반지름이 1인 사분원 위에 \( \alpha, \beta \) 각에 해당하는 \( A, B \) 점을 그려 봅니다.
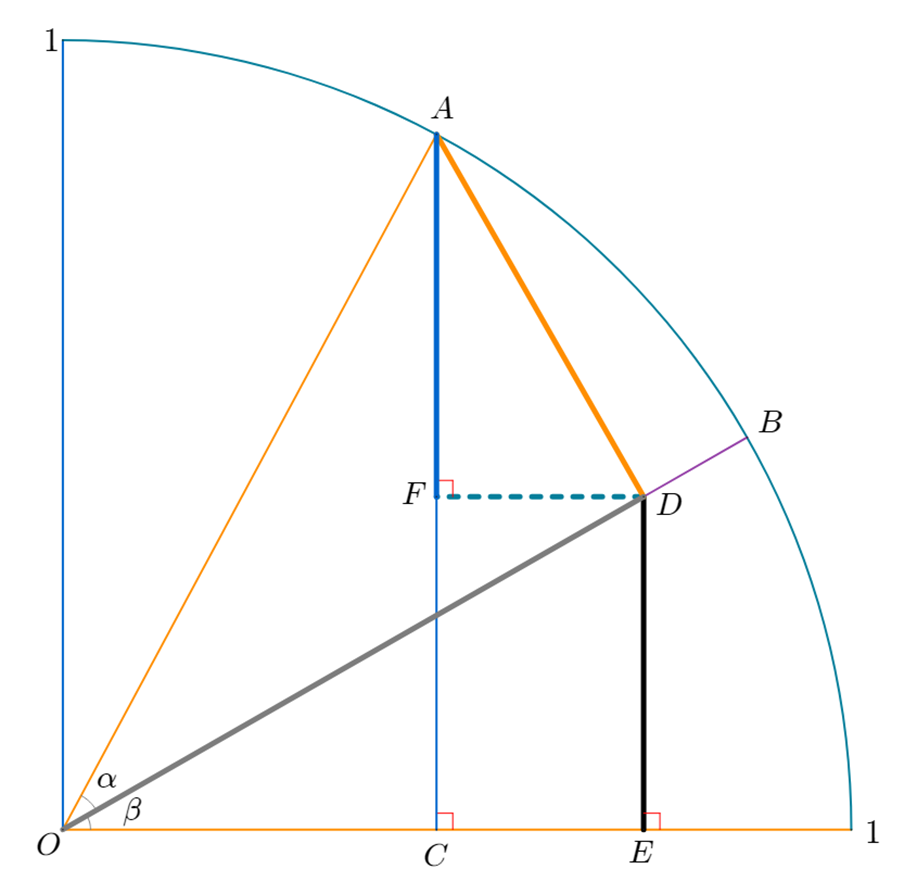
삼각함수 덧셈정리 증명
step 1 – 기본 아이디어
삼각함수(사인)의 덧셈정리 증명의 아이디어는 다음과 같습니다.
위 그림에서 \( \overline{AC} \) 의 길이는 \( \sin (\alpha + \beta) \) 입니다.
이 길이와 \( \overline{AF} + \overline{DE} \) 의 길이가 같음을 이용해서 증명하고자 합니다.
step 2 – \( \overline{AF} \)
\( \overline{AD} \) 는 \( \sin \alpha \) 입니다.
\( \overline{AF} \) 는 \( \sin \alpha \times \cos \beta \) 입니다.
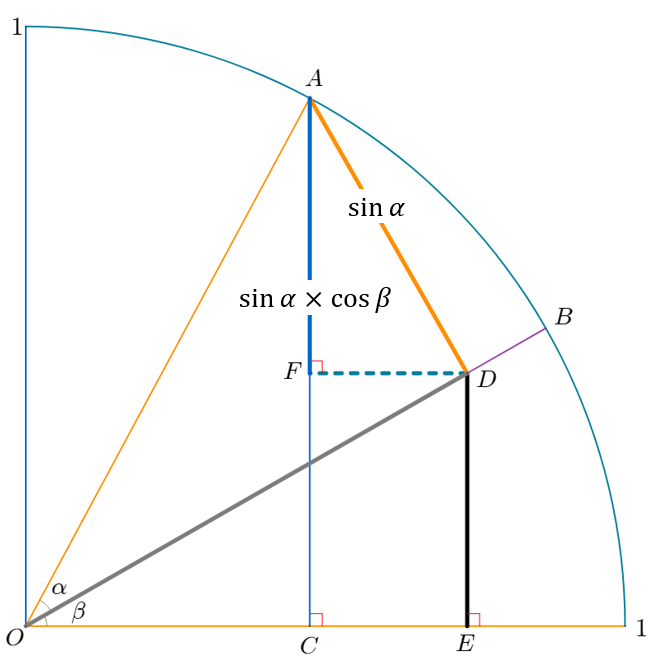
step 3 – \( \overline{DE} \)
\( \overline{OD} \) 는 \( \cos \alpha \) 입니다.
\( \overline{DE} \) 는 \( \cos \alpha \times \sin \beta \) 입니다.
\( \overline{AC} = \overline{AF} + \overline{DE} \) 이므로
\( \sin(\alpha + \beta) = \sin\alpha \cdot \cos\beta + \cos\alpha \cdot \sin\beta \) 임을 증명 하였습니다.
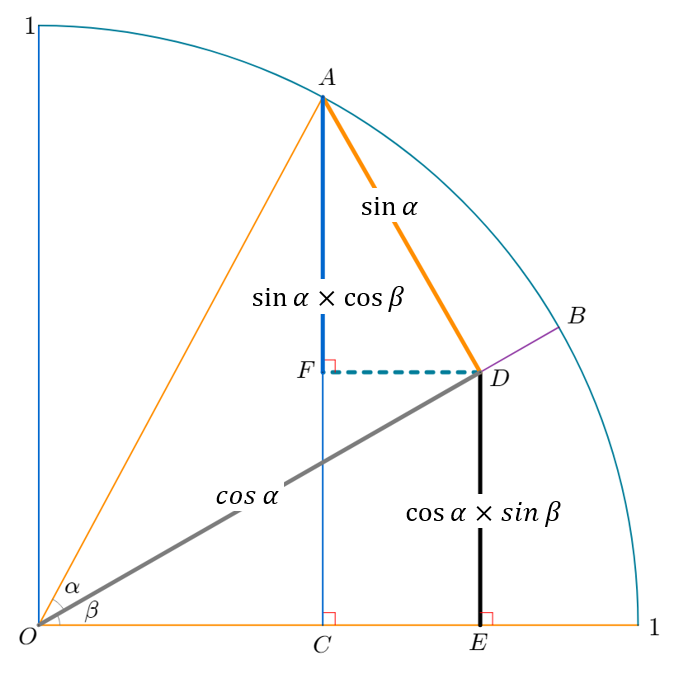
마무리
오늘은 삼각함수 사인의 덧셈정리 증명 방법에 대해서 설명 드렸습니다.
이 외의 또 다른 방법에 대해서는 다음 증명 방법으로 소개 드리도록 하겠습니다.

